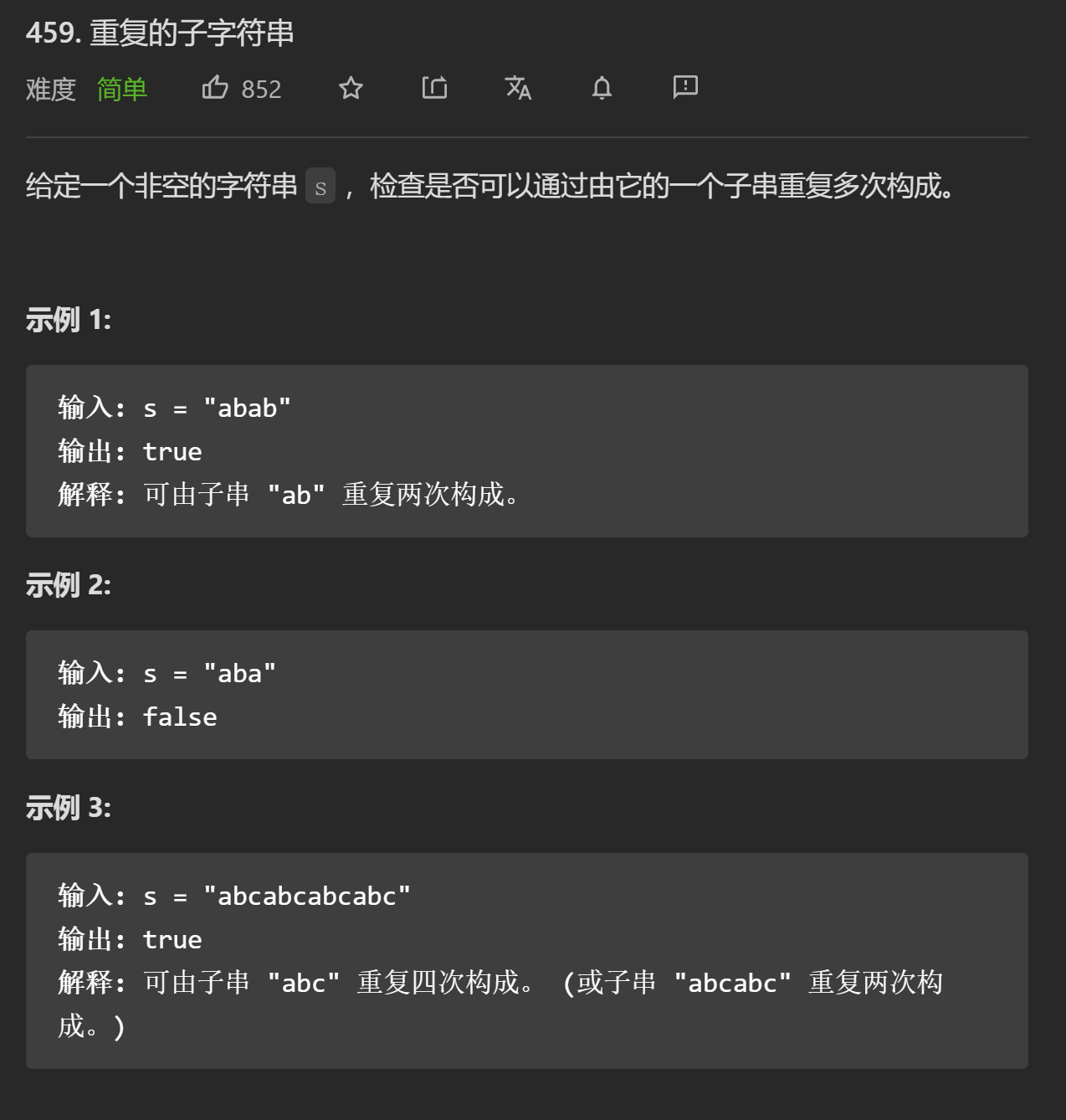
解题思路
- KML算法,计算最长相当前后缀长度,字符串长度减最长相当前后缀长度即为最小的重复字符串,字符串长度余最小重复字符串长度为0则说明字符串为重复字符串
- 将字符串相加,同时掐头去尾2个,如果新字符串包含原字符串,则说明字符串是重复字符串
KML 解题源码
1 | public boolean repeatedSubstringPattern(String s) { |
相加解题源码
1 |
|

1 | public boolean repeatedSubstringPattern(String s) { |
1 |
|
KML 算法用来处理字符串匹配的问题。核心思想是当出现字符串不匹配时,根据之前已经匹配的文本内容,避免从头再去做匹配。
字符串,原始字符串,模式串是否属于字符串的一部分;
模式串,字符串的子串,用来匹配的。
对应字符串与模式串如下:
字符串:aabaabaafa
模式串:aabaaf
暴力破解方式为2层循环,一个字符一个字符交替进行匹配,此时时间复杂度为 n * m。
使用KML算法匹配,从第一个开始匹配,匹配到b != f的时候,不是从头开始匹配,而是从模式串的b开始往后匹配,可以一直匹配的末尾,字符串匹配到最后一个的下标减模式串的长度(8-6=2),即是结果
能更清晰说明白KML算法,需要厘清几个概念
1 | /** |
  系统开发中经常遇到保护用户敏感信息的需求,比如身份证、手机号码等,在页面显示需要脱敏,在数据库保存需要加密以防止脱库等。脱敏、加密解密属于与业务无关的公共逻辑,如果夹杂在业务代码里面,不仅会增加业务代码的复杂度,而且容易出错。将其抽象提取到业务代码以外,使脱敏、加密解密对业务代码无侵入将能简化业务代码,降低出BUG的概率。
前端页面需要脱敏字段特征:
内存状态:在内存中是明文
脱敏时刻:给到前端页面那一刻脱敏
脱敏后是否还会用到该对象:脱敏后方法结束,无需再使用,即内存中的对象会被回收,即脱敏后内存状态无需关注
基于以上特点分析,可以借助spring mvc的 ResponseBodyAdvice实现。ResponseBodyAdvice接口会对加了@RestController(也就是@Controller+@ResponseBody)注解的处理器的返回值进行增强处理,底层基于AOP实现。
ResponseBodyAdvice 有2个方法supports和beforeBodyWrite,supports判断当前返回值是否需要增强处理,beforeBodyWrite实现增强处理的具体逻辑。
基于脱敏字段特征及ResponseBodyAdvice的实现方式,实现思路如下:
设计一个基类,基类包含一个字段,用以说明当前业务状态是否需要脱敏。需要脱敏的实体都继承自该基类;
设计一个注解,注解只有一个参数,说明脱敏算法类型(比如手机号码脱敏算法、邮箱脱敏算法等),需要脱敏的字段使用注解标注;
实现ResponseBodyAdvice接口的2个方法supports和beforeBodyWrite,supports通过返回值类型判断是否需要做增强处理;beforeBodyWrite根据反射获取父类判断是否需要脱敏,再通过反射获取脱敏注解的字段,将字段脱敏。
1 | /** |
1 | /** |
1 | /** |
1 | /** |
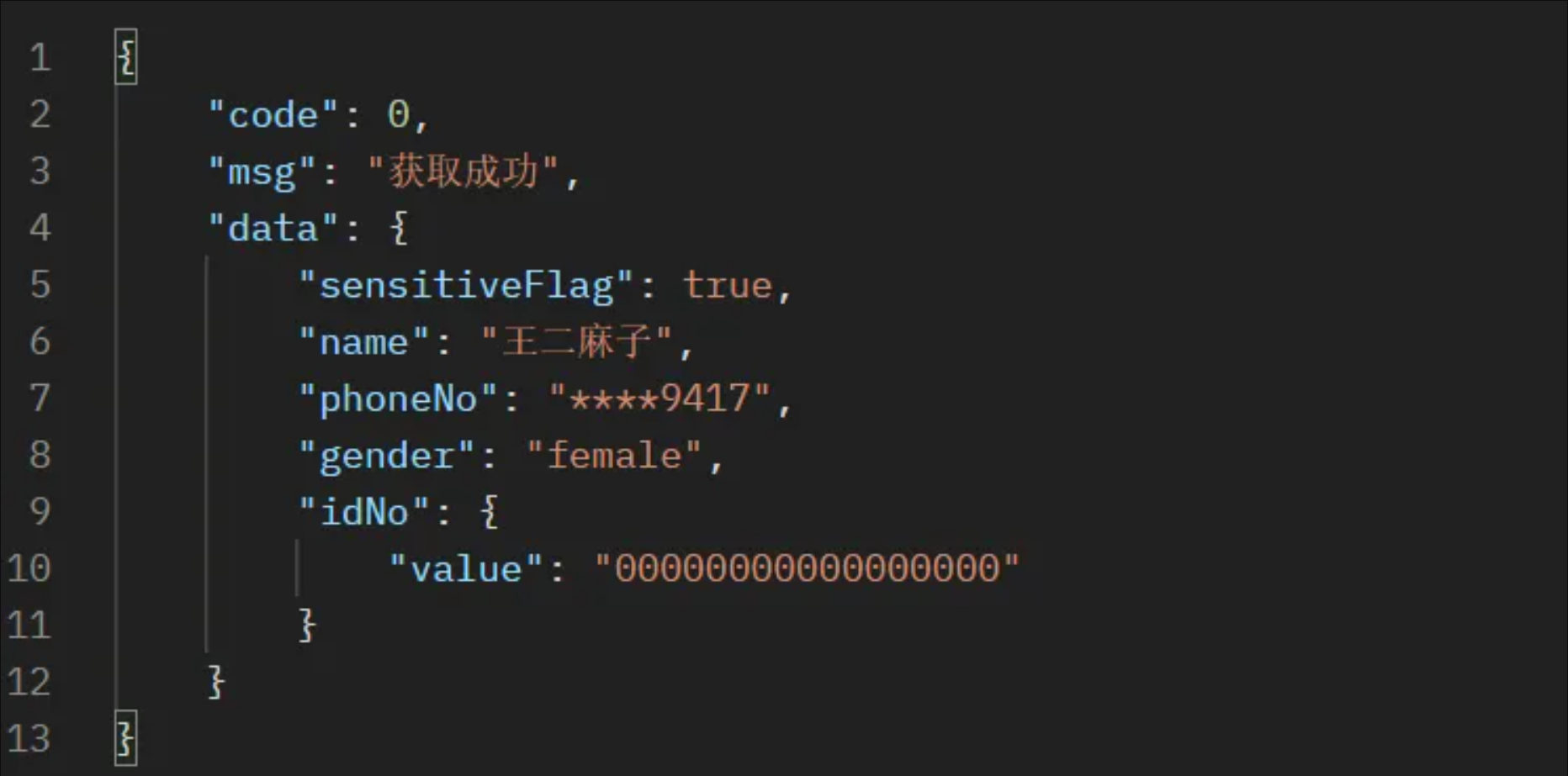
脱敏效果
数据库字段加密解密特征:
加密时刻:入库的时候
解密时刻:出库的时候
内存状态要求:在内存中需是明文
解密后是否会用到对象:会,解密即读库,读库一定是为了使用,因此解密后内存需为明文
加密后是否会用到对象:可能会,某些业务入库即结束,有些用户入库后可能还有进一步的业务,因此加密后内存中仍需保持明文。
基于以上特征分析,可以采用mybatis的Interceptor拦截器或新定义类型使用TypeHandler处理。
加密:预先对入参类通过继承基类或注解添加加密标识,拦截setParameters,获取入参对象,获取到标记为需要加密的字段,对字段内容进行加密
解密:预先对结果类通过继承基类或注解添加解密标识,拦截handleResultSets,获取查询结果对象,获取需要解密的字段,对字段进行解密
缺点:加密后会将入参对象字段改为密文,影响后续使用,需要在入库的同时再操作一次读库以保证内存中一直是明文
mybatis拦截器解密存在瑕疵,加密后需特殊处理,不建议使用,因此不再罗列该方案demo代码。
TypeHandler在mybatis中用于实现java类型和JDBC类型的相互转换。mybatis使用prepareStatement进行参数设置的时候,通过typeHandler将传入的java类型参数转换成对应的JDBC类型参数,这个过程是通过调用PrepareStatement不同的set方法实现的;在获取结果返回之后,需将返回的结果的JDBC类型转换成java类型,通过调用ResultSet对象不同类型的get方法实现;所以不同类型的typeHandler其实就是调用PrepareStatement和ResultSet的不同方法来进行类型的转换,因此可以在调用PrepareStatement和ResultSet的相关方法之前可以对传入的参数进行处理
继承BaseTypeHandler,实现setNonNullParameter方法实现加密逻辑,实现getNullableResult方法实现解密逻辑;
将与数据库交互的类中需要加密解密的字段类型用自定义的类代替;
如果需要对前端无感,可以统一对json工具做特殊处理,对加密对象的json序列化和反序列化按照字符串逻辑处理。
1 | /** |
如果使用jackson进行json序列化和反序列化,可以通过新的序列化反序列化逻辑,代码如下:
1 | // jackson |
1 | import com.qw.desensitize.dto.Encrypt; |
使用举例:
1 | /** |
加密效果:
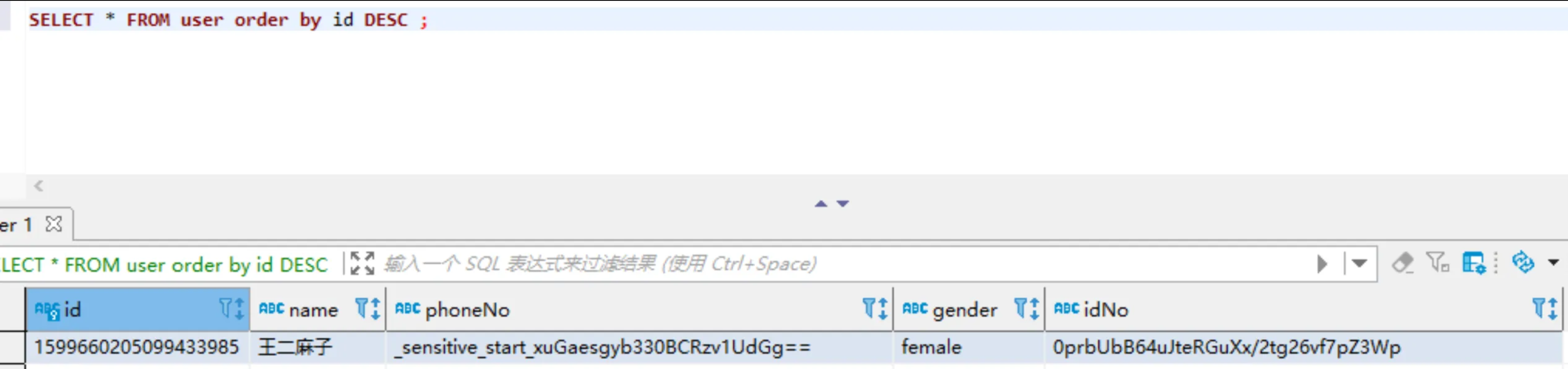
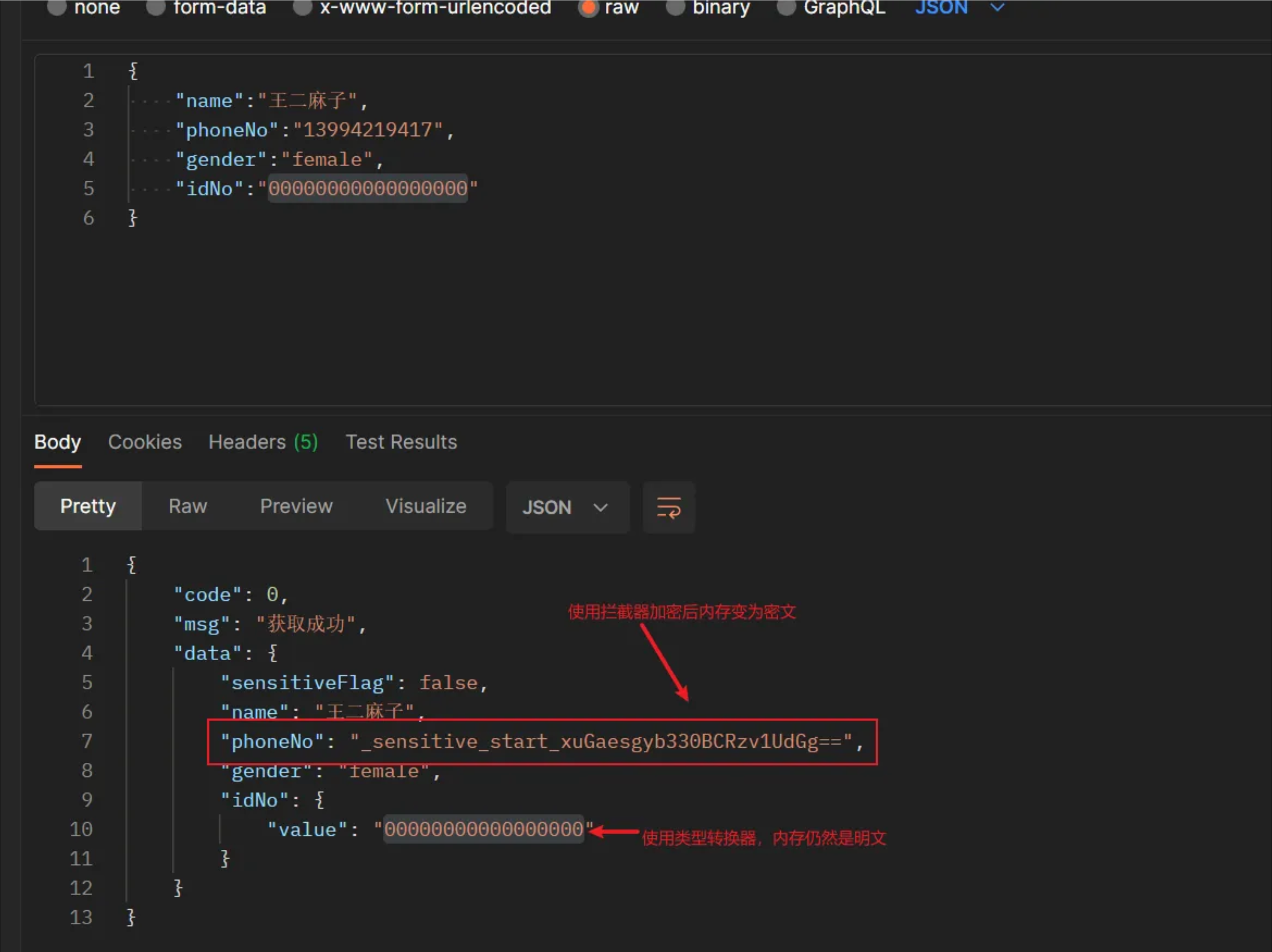
页面字段脱敏利用spring mvc 的ResponseBodyAdvice,在返回结果前改变对象为密文
数据库加密解密,既可以采用mybatis的拦截器,也可以采用mybatis的类型转换器,拦截器在加密的同时会改变内存数据为密文,mybatis类型转换器不会改变原对象
反转区间为前n的子串
反转区间为n到末尾的子串
反转整个字符串
1 | class Solution { |
Arrays.sort分基本类型排序和对象排序。基本类型排序由DualPivotQuicksort.sort实现,对象排序由TimSort.sort实现。涉及的主要算法包括TimSort、插入排序、双插入排序、双轴快排、荷兰国旗问题等。
TimSort是归并算法的改进算法
TimSort不一定比归并算法速度快,但是对部分有序的数组排序会快很多,现实中很多数据又一定程度有序,因此TimSort速度快
TimSort逻辑,将数组拆分成若干单调递增的子数组,每个子数组称为一个run,拆分完后再两两将run合并起来。拆分过程中,将每个run尽量拆分成数量相近
能被拆分成少量run的数组称为高度结构化的数组
归并时候将结果归并在临时数组,最后一次的时候再将数据拷贝回去,JDK做了优化,辅助数组轮流做,只要保证最后一次归并在主数组即可,这样可以省去最后再做数组拷贝
插入排序,每次从待排序的数字从取一个,插入到前方以有序的数组中
双插入排序,每次从待排序的数字中取两个,从大到小排序,将大的插入到前方有序的数组中,从大的数字插入的位置向前将小的数字插入
快排取一个基数,然后将数组按照基数为界分到左右两边,往复递归
双轴快排则取2个基数,将数组按照基数分左中右三遍,往复递归
荷兰国旗问题,使用双指针进行双轴快排的分区思想
1 | public void sortColors(int[] nums) { |
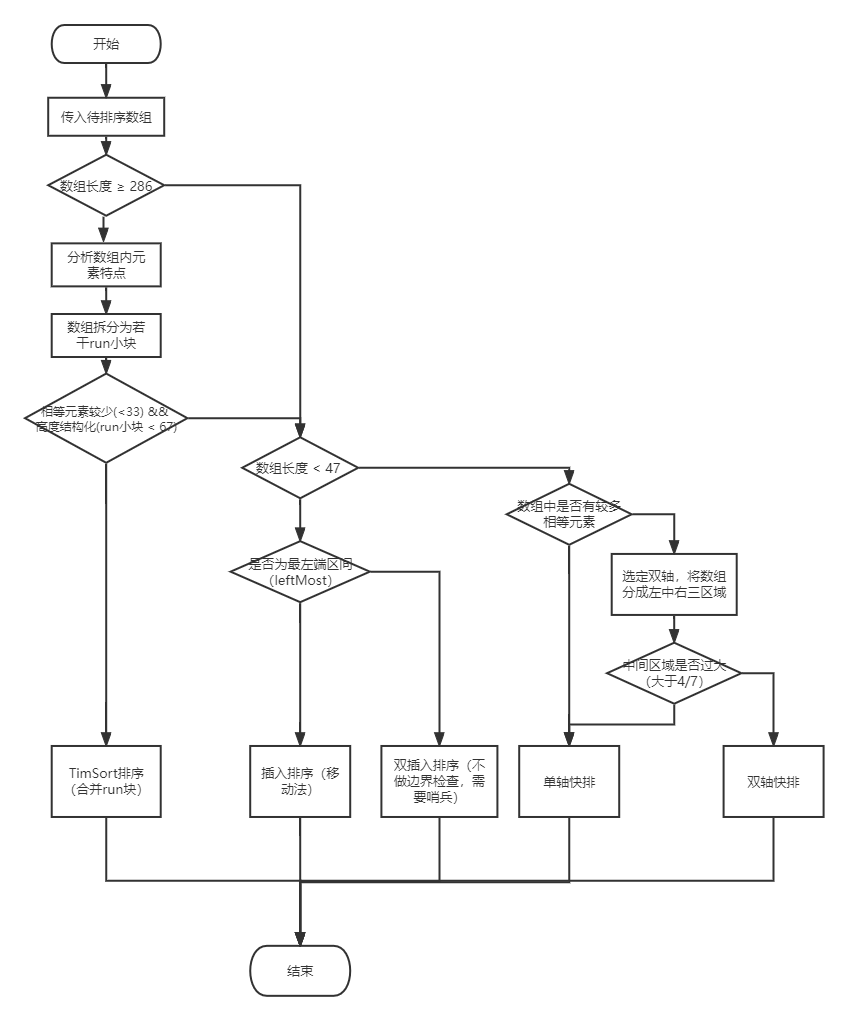
当长度大到286,MAX_RUN_LENGTH< 33,即连续相等数字小于33,MAX_RUN_COUNT < 67,即run数量小于67,则采取简化版的TimSort排序(简化版TimSort指拆分不保障每个run小块大小接近),其他情况使用 sort(a, left, right, true)
数组长度小于INSERTION_SORT_THRESHOLD=47,采用插入排序或双插入排序,其他情况采用双轴快排。如果是从最左端开始则使用插入排序,如果不是从最左端开始则使用双插入排序
1 | /** |
计算待排序数组的最大值和最小值
计数数组位最大值到最小值的长度
循环待排序数组,计数并按照值减最小是的下标放入计数数组
循环计数数组,计算每个值前面的个数和
再次循环待排序数组,找到计数小标的值,即为当前的排位,同步给排位加一(加一处理相当的情况)
时间复杂度为O(n+k),k为数组区间范围,由此可见该方法适用于区间比较短的排序,空间复杂度O(n+k)
1 | private void countingSort(int[] arr) { |
“猜数字”游戏:一方从 [1, 100][1,100] 中随机选取一个数字,另一方来猜。每次猜测都会得到「高了」或者「低了」的回答。怎样才能以最少的次数猜中呢?
二分。
二分算法能够保证每次都排除一半的数字。每次猜测不会出现惊喜(一次排除了多于一半的数字),也不会出现悲伤(一次只排除了少于一半的数字),因为答案的每一个分支都是等概率的,所以它在最差的情况下表现是最好的,猜测的一方在logn次以内必然能够猜中。
基于比较的排序算法与“猜数字”是类似的,每次比较,我们只能得到 a > ba>b 或者 a ≤ ba≤b 两种结果,如果我们把数组的全排列比作一块区域,那么每次比较都只能将这块区域分成两份,也就是说每次比较最多排除掉1/2的可能性。
计数排序算法,计数排序时申请了长度为 k 的计数数组,在遍历每一个数字时,这个数字落在计数数组中的可能性共有 k 种,但通过数字本身的大小属性,一次即可把它放到正确的位置上。相当于一次排除了 (k - 1)/k(k−1)/k 种可能性。这就是计数排序算法比基于比较的排序算法更快的根本原因。
找出最大值
计算最大值的长度,需根据最大值的长度计算基数,并对基数做比较
从尾到头或从头到尾的方式,一位一位比较,一位一位比较的时候使用计数排序,因为每一位的数字是0-9,为了处理负数,使用从-9-9的方式(如果使用0-9,负数加变正数容易引起int越界)
人排序的时候从头到尾更快,计算机排序的话从尾到头更容易
基数排序是稳定的排序
基数排序的时间复杂度为 O(d(n + k))O(d(n+k))(d 表示最长数字的位数,k 表示每个基数可能的取值范围大小)。空间复杂度为 O(n + k)O(n+k)(k 表示每个基数可能的取值范围大小)
1 | /** |
桶排序适合排序数据量很大,内存无法一次性读进去的数据
设置桶的数量
计算最大值,最小值,根据最大值、最小值、桶的数量、排序数总数量,计算每个桶边界值,(max - min) / (bucketCount - 1) 为桶之间的差值,待排序数字在桶的索引 index = (int) ((value - min) / gap)
对每个桶排序
合并桶为一个数组
1 | private void bucketSort(int[] arr) { |
时间复杂度是O(nlogn)的排序算法有希尔排序、堆排序、快排、归并排序。
取arr.length / 2 做为间隔,逐一减小间隔
按照间隔,将子数组做插入排序
构建大顶堆,从堆最后一个非叶子(数组下标 n/2 - 1)节点开始堆化,一直到堆顶
取出大顶堆的堆顶元素,与数组最后一位交换
从当前堆顶,重新堆化
随机取一个基准,即privot,将大于基准的放入右侧,小于基准的放入左侧
递归的跳出条件,start = end || start = end + 1
将大于基准放入左侧,小于基准放入右侧采用双指针法
将连个有序数组合并为一个数组
通过递归,将数组拆分为只有一个的数组
反过来,再按照合并有序数组的方式合并
时间复杂度都在O(n) ~ O($n^2$)
希尔排序、堆排序、快排是不稳定的排序,归并是稳定的排序
空间复杂度不一样,希尔排序、堆排序是O(1),快排是O(logn),归并是O(n)
归并排序是时间复杂度O(nlogn),O(n)空间复杂度的排序算法。
对两个有序数组合并成为有序数组,只需要O(n)的时间复杂度
将数组从中间拆分为2个数组,递归拆分,直到只剩一个数字
一个数字本身即为有序的,此时按照合并有序数组的方式开始合并
每次合并的数组本身就都是有序的,因此最后返回的即为有序数组
开始定义一个和排序数组长度一致的数组做为临时储存使用,这样就不用每次都创建空间了
无法进行原地排序,如果使用原地排序后即变为插入排序
归并排序也为稳定的排序算法
1 | private int[] mergeSort(int[] arr) { |
排序,取中位数即为答案
使用摩尔投票法
要获取的数据大于n/2,基于此理解。取一个数,与下一个数比较,如果想当则count+1,如果不等则count-1,等count等于0的时候,取下一个数继续该过程,最后留下的那个数一定是大于n/2的。
1 | class Solution { |
快排平均时间复杂度O(nlogn),平均空间复杂度O(logn)。效率和使用比较多的排序算法。
从数组取出一个数,叫基数(privot)
遍历数组,将数组中的数按照大于和小于基数,分布在基数的两边
将左右两个数组再次重复以上步骤,直到分成的子数组数量只要1个或2个
当某个区域只剩下一个数字或0个数字的时候就不需要排序了
start 存在 等于middle,等于middle-1;end存在等于middle,等于end-1,则start == end 或end+1 = start情况下退出递归
进一步推理,start >= end 则退出递归,因为start正常情况下都小于end
选择第一个做为基数
选择最后一个做为基数
随机选择基数,随机选择基数时间复杂度最优
简单分区算法,从left开始,遇到比基数大的,则交换到数组最后并将right减1,直到left和right相遇,再将基数和中间的数交换,返回中间值的下标
双指针分区算法
随机获取基数
防止数组正序或逆序,先将数组用洗牌算法打乱
每次从未处理的数据中,随机取一个数字,将其放入数字末尾。即JDK的Collections.shuffle()
1 | class Solution { |